Edge of the square
Not every image can and should be composed by “rules” but awareness of the underlying reasons can aid in understanding how to use them to create images that say what you intended. When composing within a square format things are slightly different than the more familiar rectangle. The image edge is even more important and in reality is part of the overall picture. What I mean by this is that the placement of the focal point is more strongly felt in a square image than a rectangle as the distance between the focal point and any one edge is easily visualized. So the balance of an image within the frame is more quickly discernible by the viewer even if only subconsciously.
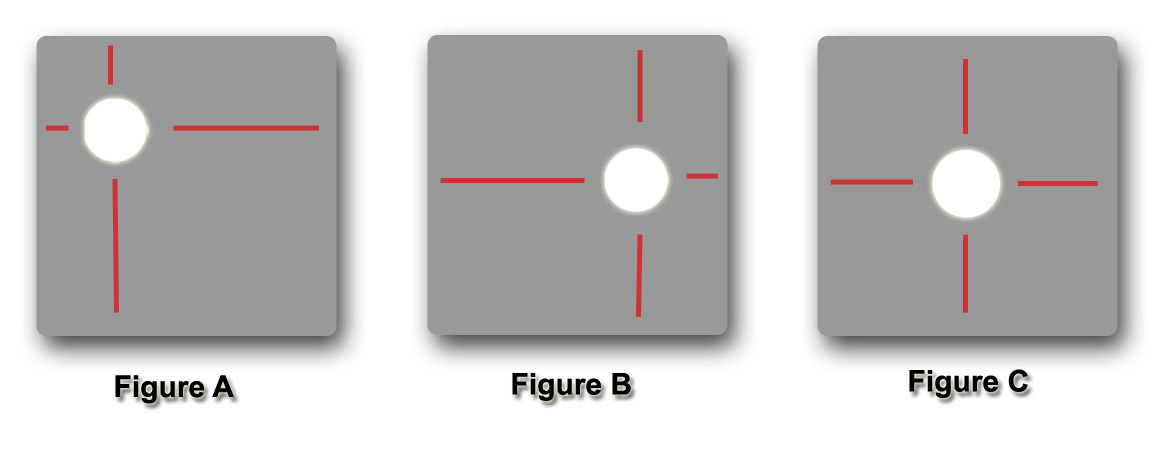
Looking at figure A it is clear that the circle, which for this illustration represents our focal point, is in a dynamic position with greater tension between the left and top edge verses the bottom and right edge.
Figure B is also unbalanced but to a lesser degree as the tension is primarily between the left and right edge of the frame.
In the final illustration Figure C you can see that the image is balanced and the competing tensions are neutralized.
When composing for rectangles we often try to avoid placing the focal point at the center of the image. With rectangles there never is truly complete balance as there is always a difference between the distances from top to bottom or left to right. The result of this is usually a very static and boring image.
Here are four examples of images shot with my cell phone that illustrate the point of balance between the subject and the frame.
You can also see that in the latter two images I have divided the image plane separately from the focal point adding to the interest of the images while keeping the focal point balanced.
More often than not this will still not produce the most dynamic composition but thinking about the picture edge and it’s effect on the image will help you create better compositions.
Don’t be afraid to break out of the box